¿y eso del Caos?. Sistemas lineales
Retomo el hilo del pedazo de charla que meti en el primer articulo alli donde me quede y releyendolo veo que he pasado por alto muchas cosas que podrian ser interesantes. Ya que no tenemos prisa y la divergencia de la trayectoria en el espacio de estado, en un sistema no lineal y con mas de dos grados de libertad lleva al sistema a un comportamiento caotico no me parece una forma correcta ni educada de acabar intentare parar en todas las posadas que hay por el camino, aunque sea por poco tiempo, para que este rimbombante enunciado, tras esas reponedoras visitas, unos ejemplos y algunos cuantos capitulos mas (espero que no tantos como las cartas de juventud de Orson a Filandrupp) quede mas claro y con el proposito de ser mas explicito en adelante. En este capitulo y en los siguientes me extendere en algunos de los diferentes conceptos que aparecen en el enunciado, me subire a ellos y mirare alrededor, e intentare explicar lo que quiere decir un sistema lineal, lo que son las ecuaciones diferenciales, que es el espacio de estado y los grados de libertad o lo que es un comportamiento caotico. Para ello habra que decir antes que es un atractor , cuando es estable o inestable, y cual es su dimension. En fin, muchas y variadas cositas que la ciencia ha tardado muchos años en recorrer y que a hombros de gigantes recorreremos en un pispas.
Necesariamente explicar algo complejo de una forma tan general y a un publico heterogeneo (suponiendo que alguien lea esto) me lleva a poner ejemplos ingenuos por un lado y poco precisos seguramente, por otro. Si sirven para iluminar el camino, aunque sea por el arcen, me dare por satisfecho. Y si alguien piensa que no son los mejores, reconozco de antemano que tendra razon. Ea! empecemos el largo camino con un pasito pequeño, como empiezan todos.
Sistemas lineales
Primeramente me centro en explicar lo que es un sistema lineal. En algebra de EGB recordareis que una recta era representada matematicamente por algo como y=a*x+b, donde a y b son numeros fijos o parametros. La diferencia entre los parametros y las llamadas variables (x dependiente e y independiente) es que estas ultimas toman todo un rango de valores mientras que los parametros permanecen fijos. Cuando a la x se le asigna toda una gama de valores numericos la y toma otro valor que viene dado por la ecuacion dada. Si se pinta sobre unos ejes lo que vemos es una linea recta donde la pendiente o inclinacion es a. Si a es muy grande la linea esta muy inclinada y si a vale 0 es justamente una linea horizontal (estos primeros ejemplos ni siquiera los pinto y con Excel podeis hacerlo). La b solo sube o baja verticalmente la linea y no le prestare mucha atencion. Lo esencial es darse cuenta de que para una anchura dx empecemos donde empecemos en el eje x le corresponde una misma anchura dy. Por ejemplo a la recta y=3x+78 le corresponde una anchura dy 3 veces mayor que la anchura dx elegida, sea cual sea esta y empiece donde empiece a contarse. Si elegimos que dx=10 contado desde x=5 (o sea desde x=5 hasta x=15) la y varia desde y=3*5+78=93 hasta y=3*15+78=123. La diferencia en y (o sea dy) vale 30, es decir 3*10. Si esto lo repetimos para cualquier otro rango de x comprobaremos que el rango de y siempre es 3 veces mayor (en general a veces)
Diremos que un sistema que verifique alguna propiedad de este estilo es un sistema lineal. Naturalmente en lugar de una ecuacion algebraica sera diferencial y en lugar de x e y representar numeros seran funciones, pero variables al fin y al cabo. Las propiedades de linealidad subyacentes, independientemenete del tipo de elementos con los que se trate, son las que importan. Mas exactamente esto; que a variaciones pequeñas de la variable INdependiente le corresponde, en una relacion constante, otra variacion pequeña de la variable DEpendiente. Explicar esto es del genero bobo pero en algun punto del camino dejareis de pensarlo.
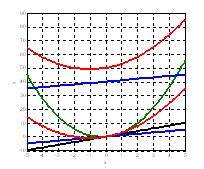
Veamos que ocurre con la siguiente curva, algo menos sencilla que una recta. Esta es la parabola, que podemos representarla por ejemplo como y=ax^2+bx+c. Para los valores a=1, b=2 y c=3 vereis que si contamos las x desde x=0 a x=10 tenemos que y varia desde y=3 a y=123 (dy=120) o sea parece como que dy=12 dx. Para ver si existe linealidad comprobemos si ese mismo 12 se mantiene al variar el rango. Si ahora variamos x desde x=0 a x=1 (dx=1) la y varia desde y=3 a y=6 (dy=3). El factor que antes era 12 ahora es un 3. Podemos hacer las pruebas que sean que siempre llegaremos a esta conclusion; deja de existir linealidad.
Los sistemas lineales son muy importantes, principalmente por 3 razones. La primera es que son sobre los que mas trabajo se ha realizado porque eran los mas simples y los unicos que se podian resolver sin ordenador (antes de 1960). La segunda se podria resumir en algo asi; "el efecto total sobre un sistema lineal es la suma de los efectos parciales" de forma que se puede resolver cada problema parcial por separado (que siempre sera mas sencillo) y despues sumarlos. La tercera razon es muy potente y es que cualquier sistema, aunque sea no lineal, presenta comportamiento lineal a pequeña escala de alguna/s de las variables y con un alcance limitado. Si nos salimos de ahi caemos en terreno resbaladizo (no existencia o unicidad de las soluciones por ejemplo). Hay bastantes mas motivos pero creo que estos son los mas rotundos. Baste con estos comentarios de momento. No quiero extenderme mas.
5 comentarios
pipo -
marta -
Despues de leerlo he vuelto al primer artículo sobre la teoría del caos que escribiste y mi impresión ha sido muy diferente. Sigue explicándolo todo poquito a poco para que pueda seguir entendiéndolo. Piensa que soy una chica que eligió letras puras, además de porque son preciosas, porque siempre vió las matemáticas como un juego (muy divertido) sin reflejo en la realidad. Qué equivocada estaba! Qué mal me transmitieron todos esos conceptos!. Quizá en octavo de EGB nuestra cabeza no da para más o no hay otra forma de explicarlo, aunque dudo ambas cosas.
Después de releerlo veo sistemas no lineales por todos lados, qué locura. Las cosas son demasiado complejas para que se repitan de forma constante en el tiempo y lo suficientemente simples para descubrir el orden dentro del caos.
macarro -
pillo -
oscar -
Estaba yo en mi pupitre, estudiando cómo podría spiderman ganar a la masa, cuando pasó algo raro. Levanté la cabeza de mis dibujos para saber qué ocurría. ¿Qué era? Era que allí, en las lejanías donde el profesor vaga habitualmente en penitente letanía, se producían sonidos e imágenes que, increíblemente, ¡eran interesantes!
Fue un momento histórico. No sé si el tal Filandrupp vivió experiencias de este tipo, pero no me preocupa porque ni siquiera sé quién es ese tío que anda últimamente en boca de todos. Cuando tenga los 23 documentos de Orson, a lo mejor opino algo, pero ahora no.
Pues sí, profe, no sé qué tecla tocó usted, que tuve la impresión de que lo que allí ocurría, en la pizarra, no solo era tan interesante como la realidad misma sin que era la propia realidad. No eran solo ecuaciones a memorizar, sino descripciones de cómo gira la luna, de cómo se proyecta una imagen en la pantalla de un televisor, de cómo llega la luz a mis ojos... ¡la revelación!
Spiderman y la masa quedaron lejos, dándose mamporros, mientras aquí llegaban la función seno, las figuras de Lissajoux, etc, de extraordinario poder visual, por cierto, a hablarnos de cómo funciona el mundo, si queremos escucharlas. Yo debo lamentar ser algo duro de oído, profe, pero capto al menos que ahí fuera hay algo que suena, y aunque hoy olvidaré los detalles concretos del sonido, mañana recordaré que al menos algo escuché, es mi sino.